La fonction "exponentielle"

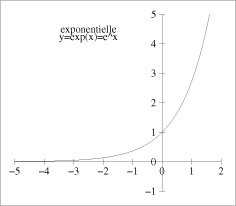
Notations	expe(x) = exp(x) = ex ( avec e ≈ 2,71828... )	exp10(x) = 10x
	ln(x) = loge(x) = logarithme naturel (ou népérien)	log(x) = log10(x) = lg(x)

Etude de la fonction e^x

	domaine de définition : Dexp = ℝ ; ex est défini ∀ x ∈ ℝ
	variation : ex est toujours croissante ( Sa dérivée est toujours positive )
	signe : ex est toujours positive.
	limite quand x → −∞ : e−∞ = 0
	e0 = 1	e1 = e
	limite quand x → +∞ : e+∞ = +∞

Propriétés :

ex est la fonction inverse de ln(x) : eln(x) = x et ln(ex) = x ; Dln=]0;∞[
ea+b = ea × eb	ea−b = ea / eb	e−a = 1 / ea
ea×b = (ea)b
dérivées	( ex )' = ex
	(eu(x))' = eu × u'	exemple : (eax+b)' = a eax+b

Applications :

• 1) décroissance radioactive : nombre d'atome restants = N(t) = N₀ e^−λt
  dN/dt = −λ N₀ e^−λt = −λ N
  dN = −λ N dt   (négatif, proportionnel au nombre d'atomes N et à la durée dt)
  période τ ou demi-vie : N(τ) = N₀ e^−λτ = N₀/2
  e^−λτ = 1/2   ⇒   −λτ = −ln(2) soit : τ = ln(2)/λ
  Le nombre d'atomes présents diminue de moitié à chaque période τ
  exemple : après 10 périodes, le nombre d'atomes sera divisé par 2¹⁰ = 1024
• 2) décharge d'un condensateur : circuit électrique RC série

  --------------	(+q| C |−q)	--------------	[R]	--------------
  i →	← U(C) ←	i →	← U(R) ←	i →
  	U(C)=q/C		U(R)=Ri

  Circuit fermé : U(C) + U(R) = 0 = q/C + Ri = q/C + R dq/dt = 0
  le signe de i dépend des positions de q et −q : ici, quand i > 0, q ↗ donc i = +dq/dt
  Condition Initiale : t=0 ; q=q(0)
    ( remarque : i(0) = q'(0) = −q(0)/(RC) )
    dq/dt + (1/(RC)) q = 0   ⇒   q(t) = q(0) e^−t/(RC)
    i(t) = dq/dt = −q(0)/(RC) e^−t/(RC)
  Avec ce choix du sens de i, comme le condensateur se décharge, i = +dq/dt < 0
• intégration de l'équation différentielle dq/dt + (1/(RC)) q = 0 :
  dq/dt = − (1/RC) q
  dq/q = (−1/RC) dt
  primitives : ∫ dq/q = ∫ (−1/(RC)) dt
  ln(q(t)) − ln(q(0)) = (−1/RC) (t − 0)
  ln(q(t)/(q(0)) = −t/(RC)
  application de exponentielle : q(t)/(q(0) = e^−t/(RC)

retour aux menus :     exponentielles     exp/log     math