développement des fonctions sin(x) et cos(x)

• Nous recherchons une fonction polynomiale P(x) qui est très voisine de sin(x) autour de x = 0
• Nous allons étudier les variations et les signes des fonctions dans [−π/2 ; π/2]
• Nous partons de la fonction sin(x)
  rappel : (sin x)' = cos x   et   (cos x)' = − sin x
  factorielle(n) = n! = 1 × 2 × 3 × 4 × . . . × n   (exemples : 3! = 6 et 5! = 120)
• pour passer d'une ligne à la suivante : par exemple : sin(x)   →   (− cos(x) + 1) :
  • on cherche à minimiser f(x) = sin(x) − P(x) au voisinage de x = 0   (ainsi que cos(x) − Q(x))
    on prend f(0) = 0
  • On recherche une primitive de f(x) = sin(x) : F(x) = ∫ sin(x) dx = − cos(x) + k
    on choisit k tel que F(0) = − cos(0) + k = 0 en x = 0   ⇒   k = cos(0) = 1
• Développements successifs de sin(x) et cos(x) au voisinage de x = 0 :

  f(x)	F(x)	F(0) = 0
  sin(x)	−cos(x) + k	k = cos(0) = 1
  −cos(x) + 1	−sin(x) + x + k	k = sin(0) = 0
  −sin(x) + x	cos(x) + x2/2 + k	k = −cos(0) = −1
  cos(x) + x2/2 − 1	sin(x) + x3/3! − x + k	k = −sin(0) = 0
  sin(x) + x3/3! − x	−cos(x) + x4/4! − x2/2 + k	k = cos(0) = 1
  −cos(x) + x4/4! − x2/2 + 1	−sin(x) + x5/5! − x3/3! + x + k	k = sin(0) = 0
  −sin(x) + x5/5! − x3/3! + x	cos(x) + x6/6! − x4/4! + x2/2 + k	k = −cos(0) = −1
  cos(x) + x6/6! − x4/4! + x2/2 − 1	sin(x) + x7/7! − x5/5! + x3/3! − x + k	k = −sin(0) = 0
  sin(x) + x7/7! − x5/5! + x3/3! − x

  Si l'on compare P(x) = x − x³/3! + x⁵/5! − x⁷/7!   à la fonction sin(x) l'écart sur [−π/2 ; π/2] est infime.
  P(x) = x − x³/3! + x⁵/5! − x⁷/7!   est le développement de sin(x) à l'ordre 7 au voisinage de x = 0
  
• Étude de la fonction : f(x) = sin(x) + x⁷/7! − x⁵/5! + x³/3! − x   sur [−π/2 ; π/2]
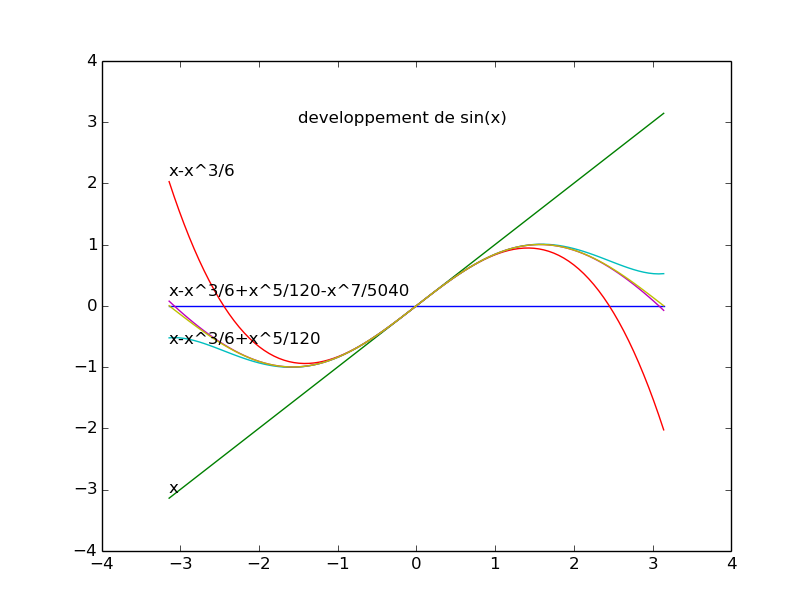
  on calcule les 8 dérivées successives de f(x) jusqu'à ce que l'on trouve une fonction connue : sin(x)
  à partir du signe de cette fonction sin(x), on déduit la variation de sa primitive.
  à partir de la variation de la primitive, on déduit son signe.
  . . . de proche en proche, on arrive à la variation de f(x)

  fonction		étude de la fonction sur [−π/2, π/2]
  		−π/2		0		π/2
  f8(x) = sin(x)	variation	−1	↗	0	↗	+1
  	signe		−	0	+
  f7(x) = −cos(x) + 1	variation	+1	↘	0	↗	+1
  	signe		+	0	+
  f6(x) = −sin(x) + x	variation	−0.57	↗	0	↗	+0.57
  	signe		−	0	+
  f5(x) = cos(x) + x2/2 − 1	variation	+0.23	↘	0	↗	+0.23
  	signe		+	0	+
  f4(x) = sin(x) + x3/3! − x	variation	−0.075	↗	0	↗	+0.075
  	signe		−	0	+
  f3(x) = −cos(x) + x4/4! − x2/2 + 1	variation	+0.020	↘	0	↗	+0.020
  	signe		+	0	+
  f2(x) = −sin(x) + x5/5! − x3/3! + x	variation	−0.005	↗	0	↗	+0.005
  	signe		−	0	+
  f1(x) = cos(x) + x6/6! − x4/4! + x2/2 − 1	variation	+0.001	↘	0	↗	+0.001
  	signe		+	0	+
  f(x) = sin(x) + x7/7! − x5/5! + x3/3! − x	variation	−0.0002	↗	0	↗	+0.0002
  	signe		−	0	+

  Dans l'intervalle [−π/2 ; π/2], l'écart entre sin(x) et P(x) = x − x³/3! + x⁵/5! − x⁷/7! est inférieur à 0,0002

Retour au menu :   Primitives   math   accueil