Parabole

• Une parabole a une équation de la forme f(x) = a x² + b x + c     ( polynôme de degré 2 : a ≠ 0 )
  • que l'on peut mettre sous la forme simple (canonique) : f(x) = a (x − x_S)² + y_S
    où le point ( x_S, y_S ) est le sommet de la parabole
  • La forme canonique peut se mettre sous la forme : f(x) = a [ (x − x_S)² − (−y_S / a) ] = a [ A² − B² ]
    prête à être factorisée si : B² = (−y_S / a) > 0
    afin d'obtenir une différence de 2 carrés.
  • que l'on peut factoriser sous la forme : f(x) = a (x − x₁) ( x − x₂)
    s'il y a des racines x₁ et x₂ à l'équation f(x) = 0
    x_1,2 = (−b ±√Δ) / (2 a)
• Variation de la fonction f(x) = a x² + b x + c
  • x_S = −b / (2a)
  • y_S = −Δ / (4a)   avec   Δ = b² − 4 a c
  • f(x) = a (x − x_S)² + y_S
    • f(x) est la parabole y = a x² déplacée de (x_S, y_S)
      
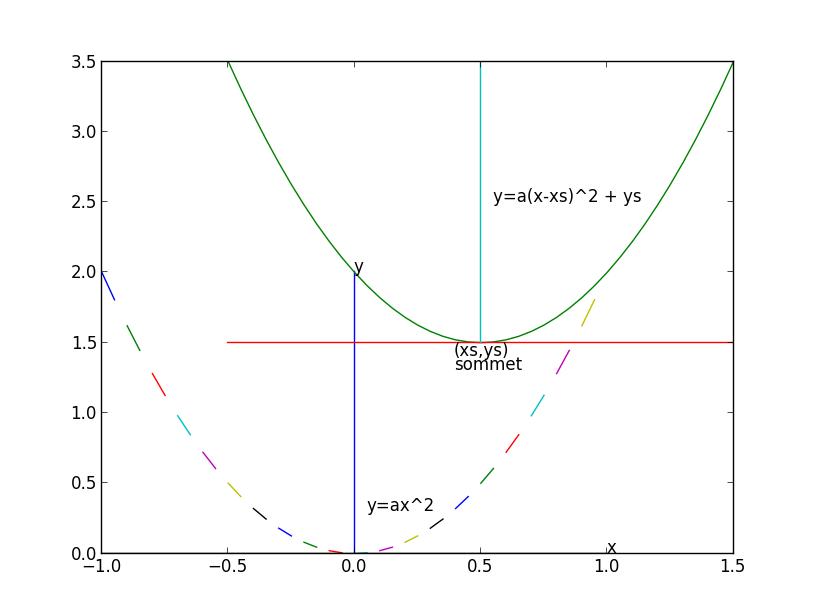
    • si a > 0 : a (x − x_S)² ≥ 0   et il devient nul pour x = x_S. On a alors f(x_S) = y_S
      le point (x_S, y_S) est le point le plus bas, c'est le sommet de la parabole.
    • si a < 0 : a (x − x_S)² ≤ 0   et il devient nul pour x = x_S. On a alors f(x_S) = y_S
      le point (x_S, y_S) est le point le plus haut, c'est le sommet de la parabole.
  • si a > 0 : forme en U
    • décroissant sur l'intervalle : ] −∞ ; x_S [
    • croissant sur l'intervalle : ] x_S ; +∞ [

      x	−∞	xS	+∞
      variation de f(x)	décroissant	minimum yS	croissant

  • si a < 0 : forme en bosse ∩
    • croissant sur l'intervalle : ] −∞ ; x_S [
    • décroissant sur l'intervalle : ] x_S ; +∞ [

      x	−∞	xS	+∞
      variation de f(x)	croissant	maximum yS	décroissant

  • quand x devient infini, (a x²) est plus grand que les 2 autres termes.
    C'est lui qui impose le signe de f(x) : pour x = ± ∞ : f(x) est du signe de a
• La parabole coupe-t-elle l'axe Ox ?
  • la fonction f(x) = a (x − x_S)² + y_S peut-elle être nulle ?
    • f(x) = 0 si (x − x_S)² = −y_S / a ≥ 0
    • si −y_S / a = −[−Δ / (4a)] / a = Δ / (4a²) ≥ 0
    • si Δ ≥ 0 : la parabole coupe l'axe Ox
• Tableau de signe de la fonction f(x) = a x² + b x + c
  • Si la parabole ne coupe pas l'axe Ox : elle reste toujours du même côté
    si Δ < 0 : f(x) est toujours du signe de a.
  • Si la parabole coupe l'axe Ox : elle change de signe lors de la traversée de l'axe Ox :
    si Δ > 0 : f(x) est du signe de a en dehors des racines,
    et du signe contraire de a entre les racines
  • Si la parabole touche simplement l'axe Ox : elle devient nulle en ce point, mais repart du même côté
    si Δ = 0 : f(x) est du signe de a sauf pour le point sur l'axe où elle est nulle.
• Si Δ > 0, il y a 2 racines à l'équation f(x) = 0
  f(x) peut se factoriser en : f(x) = a (x − x₁) ( x − x₂)
  • calcul des racines :
  • f(x) = a [ (x − x_S)² + y_S / a ]
  • comme ( y_S / a ) < 0   :   f(x) = a [ (x − x_S)² − (√ −y_S / a )² ]
    en appliquant l'identité remarquable : A² − B² = ( A − B ) ( A + B ) :
    f(x) = a ( x − x_S − √ −y_S / a ) ( x − x_S + √ −y_S / a )
    où x₁ = x_S + √ −y_S / a   et   x₂ = x_S − √ −y_S / a
  en appelant x₁ la plus petite des 2 racines : x₁ < x₂

  x	−∞	x1		x2	+∞
  signe de a	signe de a		signe de a		signe de a
  signe de (x − x1)	−	0	+	+	+
  signe de (x − x2)	−	−	−	0	+
  signe de f(x)	signe de a	0	− signe de a	0	signe de a

  • f(x) est du signe contraire de a pour x appartient à ] x₁ ; x₂ [ (intervalle)
  • f(x) = 0 pour x appartient à { x₁, x₂ } (ensemble)
  • f(x) est du signe de a pour x appartient à ] −∞ ; x₁ [ U ] x₂ ; +∞ [
• Si Δ = 0, il y a 1 racine (double) à l'équation f(x) = 0
  f(x) peut se factoriser en : f(x) = a (x − x₁) ( x − x₁ ) = a ( x − x₁ )²

  x	−∞	x1	+∞
  signe de a	signe de a		signe de a
  signe de (x − x1)2	+	0	+
  signe de f(x)	signe de a	0	signe de a

  • f(x) = 0 pour x = x₁
  • f(x) est du signe de a pour x appartient à ] −∞ ; x₁ [ U ] x₁ ; +∞ [
• Si Δ < 0, il y a 0 racine à l'équation f(x) = 0

  x	−∞         +∞
  signe de a	signe de a
  signe de f(x)	signe de a

  • f(x) est du signe de a pour x appartient à ] −∞ ; +∞ [

retour au menu :   1ère ES   freescience