Vecteurs dans le plan 2D [répertoire]

• un vecteur AB : soient 2 points : A=(x_A, y_A) et B=(x_B, y_B)
  • c'est une flèche qui va de A à B (A→B)
    ( je mets la flèche entre les deux car je ne peux pas la mettre au-dessus )
    ( je mets aussi les vecteurs en caractère gras : i, j, u, v, V )
  • exemples (en physique) : la force, la vitesse, le déplacement
  • On dit, pour le vecteur, son origine A et son extrémité B.
  • si on échange les extrêmités, le vecteur change de signe : (A→B) = − (B→A)
• Un vecteur est caractérisé par :
  • sa direction (la direction de la droite qui le porte)
  • son sens (d'un côté ou de l'autre)
  • son module (sa longueur = la distance AB)
• Un vecteur peut être déplacé par translation : c'est toujours le même vecteur.
• Dans un parallélogramme ABCD (les points étant marqués en tournant A, B, C, D, A) :
  
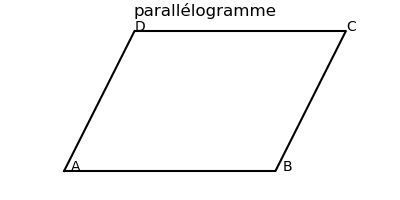
  • on a : (A→B) = (D→C) ainsi que (B→C) = (A→D).   (vérifier l'ordre des extrêmités sur une figure)
    ou bien : (A→B) = − (C→D) ainsi que (B→C) = − (D→A)
  • Inversement : si (A→B) = (D→C), alors ABCD est un parallélogramme
      car les 2 côtés opposés sont parallèles et égaux.
    ou bien si (B→C) = (A→D), alors ABCD est un parallélogramme
    une seule des 2 conditions suffit.
• 2 opérations sur les vecteurs :
  • addition :
    Pour additionner 2 vecteurs, on les met bout à bout : A→B + B→C = A→C (relation de Chasles)
  • produit par un nombre (on dit aussi un scalaire) :
    3 (A→B) = (A→B) + (A→B) + (A→B)   (mis bout-à-bout)
    direction : k (A→B) ne change pas la direction du vecteur (A→B)
    sens : k (A→B) : si k > 0 : ne change pas le sens du vecteur (A→B) ; si k < 0 : retourne le vecteur
    module : k (A→B) a pour module : |k| × AB
• 2 vecteurs u et v sont colinéaires (ou proportionnels)   ⇔   ∃ k tel que : v = k u

  ---

• On peut exprimer les vecteurs par rapport à un repère ou une base
  • Base du plan : une origine O et 2 vecteurs i et j   (qui ne sont pas colinéaires)
    coordonnées de l'origine : O=(0, 0)
    V = x i + y j   avec les coordonnées : V = (x, y) dans la base (O, i, j)
  • Addition de 2 vecteurs : V₁=(x₁, y₁) et V₂=(x₂, y₂)
    V₁ + V₂ = (x₁+x₂, y₁+y₂)
    soit : V₁ + V₂ = (x₁+x₂) i + (y₁+y₂) j
  • Multiplication par un scalaire (réel) a ∈ R : a V = (ax, ay) = (ax) i + (ay) j
    vecteur opposé : V × (−1) = −V = (−x, −y)
    vecteur nul : V × 0 = 0   (vecteur 0)
• vecteur reliant 2 points A et B :
  • (A→B) = (x_B − x_A) i + (y_B − y_A) j
    ( abscisse de l'extrêmité − abscisse de l'origine ) ← à apprendre par coeur !
    toujours : extrêmité − origine : A→B = B − A
    d'où (A→B) + (B→C) = B − A + C − B = C − A = (A→C)
    remarque : point A = (O→A)
• 2 vecteurs u=(x, y) et v=(x', y') sont colinéaires (ou proportionnels)   ⇔   ∃ k tel que : v = k u

  Soit, en coordonnées, en éliminant k :	x'	= k x	× (−y)
  	y'	= k y	× x
  	x y' − y x'	= 0

  ou encore : x y' = x' y   ⇔   les vecteurs u=(x, y) et v=(x', y') sont colinéaires.

  ---

• Le repère est orthonormé si :
  • i perpendiculaire à j (ortho)
  • i et j sont tous les deux de longueur 1 (ou unité) (ou normé)
  • Alors la longueur (ou module) du vecteur V=(x, y) est : V = √x² + y²
    (d'après le théorème de Pythagore)

  ---

• Cours de l'île aux maths (seconde) : vecteurs du plan
• Exercices de la page (seconde) : vecteurs de l'espace 3D ( rubrique : repérage et vecteurs )
• Exercice : Dans une base orthonormée (O(0,0), i, j) du plan, soient les 2 points : A=(2,3) et B=(3,2)
  • tracer les points ainsi que le vecteur A→B
  • calculer les coordonnées du vecteur A→B ? réponse
  • calculer son module ? réponse   (on peut appliquer cette formule car la base est orthonormée)
  • Soit le vecteur V=(2,4), calculer le vecteur A→B + V ? réponse
  • trouver le point C tel que A→C = V ? réponse
  • trouver le point D tel que O→D = 3 A→B ? réponse
  • vérifier que A→B et O→D sont colinéaires ? réponse

retour aux menus :   géométrie   math