Math. Construction de Perpendiculaires et de Parallèles

• Tracer un triangle équilatéral : 3 côtés égaux ; 3 angles égaux à 60°
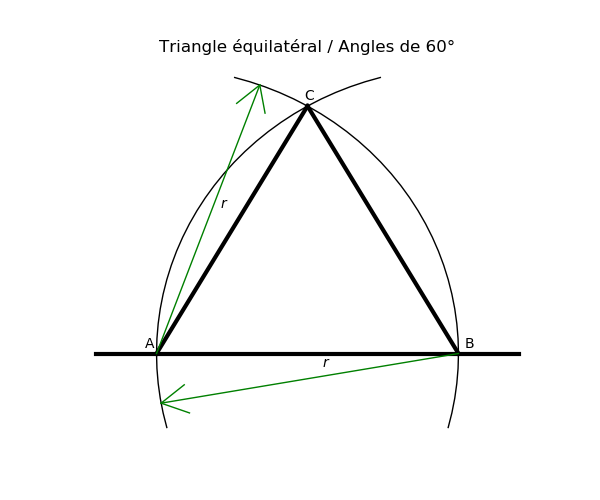
  On part d'une droite sur laquelle, on choisit un point A
  On trace un cercle de centre A et de rayon r : le point B est l'intersection du cercle avec la droite
  On trace un cercle de centre B et de rayon r : Le point C est l'intersection des 2 cercles
  
   
• Tracer la perpendiculaire à une droite (d) passant par un point A de cette droite :
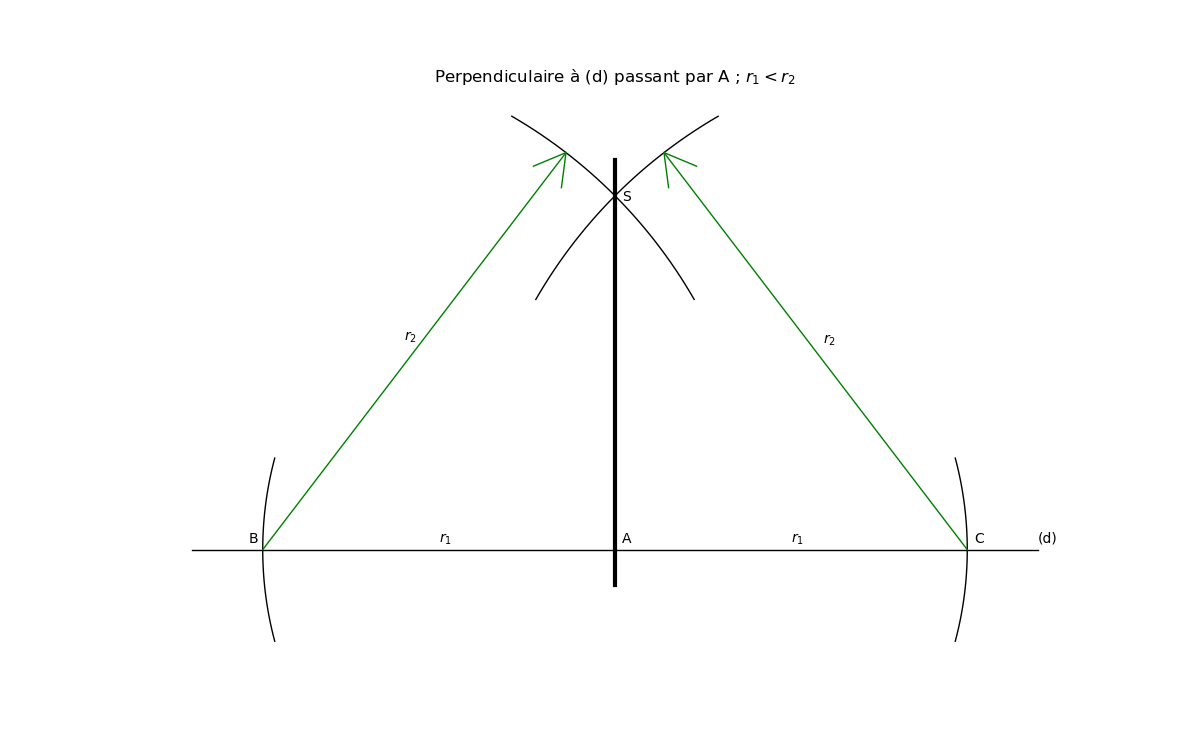
  On construit un triangle isocèle de sommet S dont le point A est le milieu du côté opposé au sommet S
  1) au compas, on reporte la même longueur r₁ à gauche et à droite de A sur la droite (d) : points B et C
  on obtient ainsi la base du triangle isocèle : [BC], A étant le milieu de la base.
  2) au compas, on construit les 2 côtés égaux du triangle isocèle en augmentant l'écartement du compas (r₂ > r₁)
  (par exemple r₂ = 1,5 r₁)
  les cercles de centres B et C se coupent au sommet S
  3) Dans un triangle isocèle, la médiane issue du sommet est aussi hauteur :
  La droite (AS) est perpendiculaire à (d) au point A
  
   
  On peut aussi construire un angle de 90° en A partant de (d) : 60°, puis la moitié de 60°.

  angle (ABC) = 60° ; le triangle (ABC) est équilatéral angle (ACD) = 60° ; le triangle (ACD) est équilatéral (AE) est la bissectrice de l'angle (CAD) : angle (CAE) = 30° angle (BAE) = 90°

   
• Tracer la perpendiculaire à une droite (d) passant par un point A en dehors de cette droite :
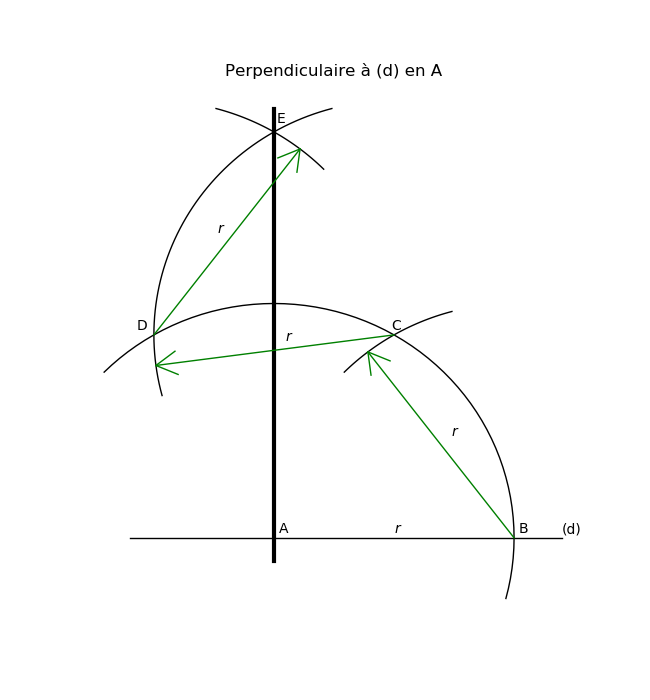
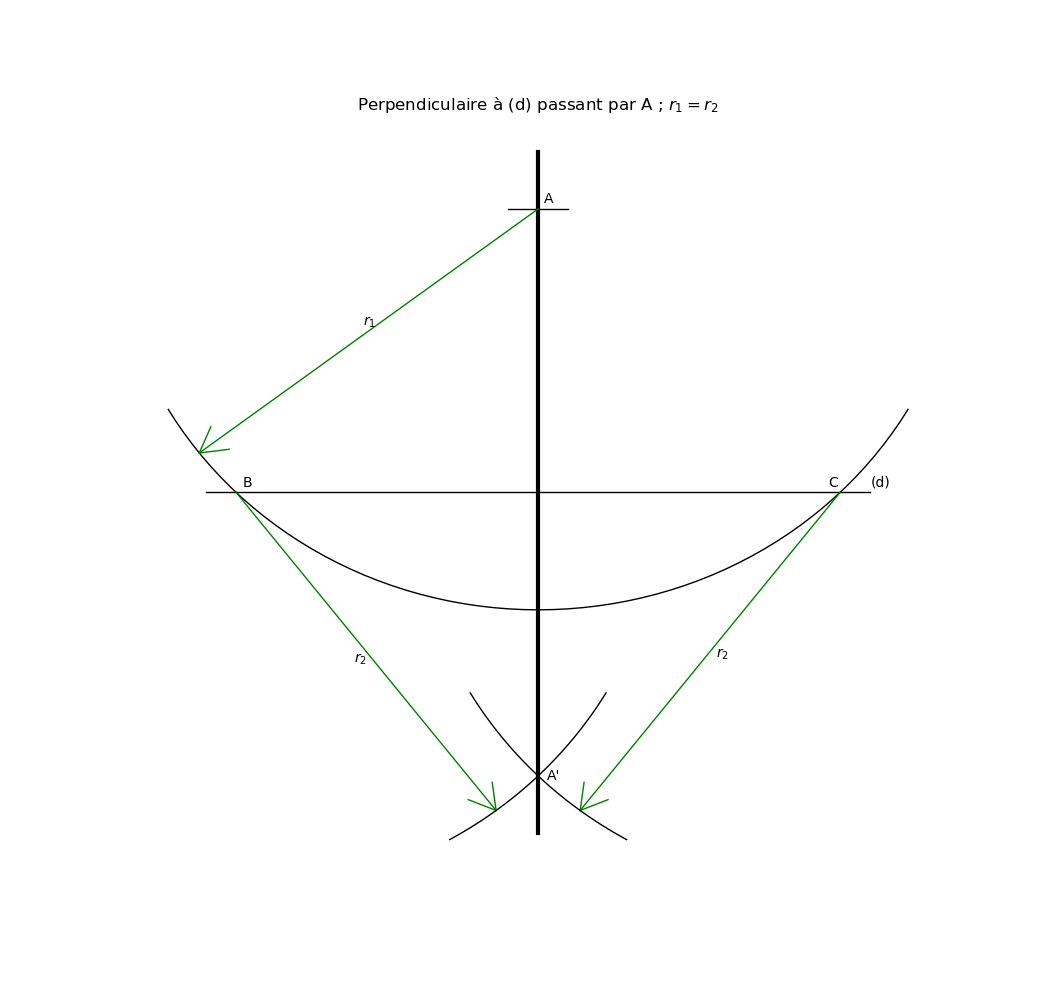
  On construit un triangle isocèle de sommet A, puis un losange par symétrie.
  1) on trace un cercle de centre A et de rayon r₁ > δ = la distance de A à (d)
  (par exemple r₁ = 1,5 δ)
  ce cercle coupe (d) en B et C : le triangle ABC est isocèle.
  2) on construit un triangle isocèle symétrique de l'autre côté de la droite
  les cercles de centres B et C se coupent en A et en A'
  3) on obtient un losange : Dans un losange, les diagonales sont perpendiculaires
  La droite (AA') est la perpendiculaire à (d) passant par le point A
  remarque 1 : le deuxième triangle (A'BC) doit être isocèle, mais peut être différent du premier
  remarque 2 : la droite (AA') est la médiatrice du segment [BC]
  
   
• Tracer la parallèle à une droite (d) passant par un point A en dehors de cette droite :
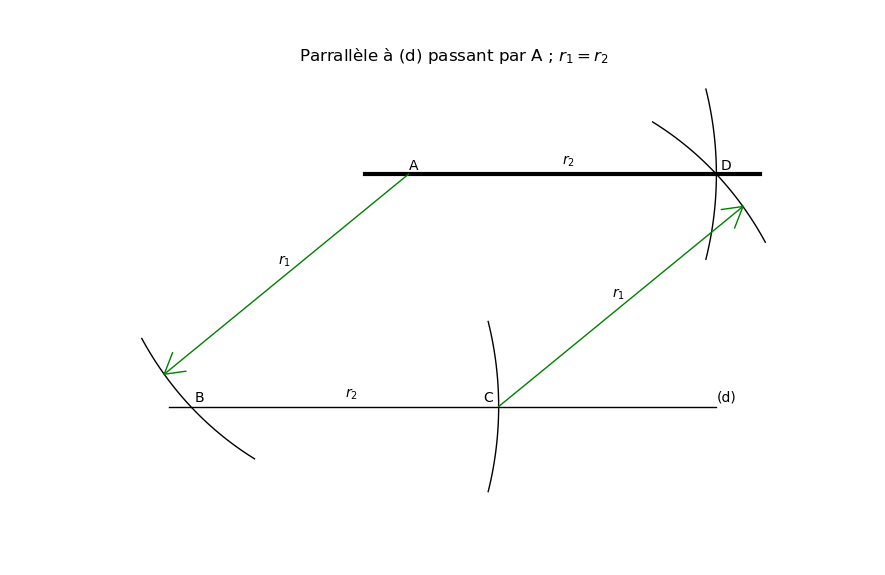
  ( tracé d'un parallélogramme ABCD )
  On construit un parallélogramme ou un losange ayant A comme sommet et (d) comme côté
  1) du point A, on trace un cercle de rayon r₁ plus grand que la distance de A à (d) qui coupe (d) en B
  2) on trace un cercle de centre B et de rayon r₂ (qui peut être égal à r₁) qui coupe (d) en C
  3) on trace un cercle de centre A et de rayon r₂ et un cercle de centre C et de rayon r₁
  ces cercles se coupent en D
  d'après la construction : AD = BC = r₂ et AB = DC = r₁
  4) (ABCD) est un parallélogramme : les côtés [AD] et [BC] sont parallèles
  de même, les côtés [AB] et [DC] sont parallèles.
  La droite (AD) est la parallèle à (d) passant par A
  

retour au menu :   géométrie   math  
file:///home/jacques/Dropbox/